Coordinate Transformation Problem

问题简述

使用向量四元数组合(Vector-Quaternion Composition)进行变化计算时,当父节点施加旋转后,其子节点的非均匀缩放会因坐标系变化而导致缩放效果发生非预期的变化。

对于非均匀缩放,Unity2022和UE5.4的处理方式如下所示。

UE5.4采用向量四元数组合计算的方式。这导致的现象是:当父节点Actor2应用非均匀缩放(例如仅沿其局部X轴缩放)时,由于子节点Actor4受到其父节点Actor3的旋转影响(如绕Y轴旋转90度),所以子节点在其父节点Actor2坐标系下缩放变化的不再是期望的X轴了,而是Z轴。这将导致如下问题。

而Unity的处理方式为:在cube节点下缩放x轴,无论cube1节点如何旋转,其子节点cube2在父节点cube坐标系下改变的都是x轴位移。

原因

该问题是因为UE5.4中基于父节点坐标系进行的向量/四元数变化组合计算。具体而言,当Scale发生变换后,在计算世界位置时,其坐标系始终基于父节点的原始空间下。因此,该计算会受到父节点旋转的影响。且非均匀缩放本身具有方向性,在各个坐标轴向上变化量并不相同。

如下UE5.4中FTransform乘法的运算代码:


x
// 节点Transform更新:
FTransform USceneComponent::CalcNewComponentToWorld_GeneralCase(const FTransform& NewRelativeTransform, const USceneComponent* Parent, FName SocketName) const
{
    if (Parent != nullptr)
    {
        const FTransform ParentToWorld = Parent->GetSocketTransform(SocketName);
        FTransform NewCompToWorld = NewRelativeTransform * ParentToWorld;
        if(IsUsingAbsoluteLocation())
        {
            NewCompToWorld.CopyTranslation(NewRelativeTransform);
        }

        if(IsUsingAbsoluteRotation())
        {
            NewCompToWorld.CopyRotation(NewRelativeTransform);
        }

        if(IsUsingAbsoluteScale())
        {
            NewCompToWorld.CopyScale3D(NewRelativeTransform);
        }

        return NewCompToWorld;
    }
    else
    {
        return NewRelativeTransform;
    }
}

/** Returns Multiplied Transform of 2 FTransforms **/
template<typename T>
FORCEINLINE void TTransform<T>::Multiply(TTransform<T>* OutTransform, const TTransform<T>* A, const TTransform<T>* B)
{
    A->DiagnosticCheckNaN_All();
    B->DiagnosticCheckNaN_All();

    checkSlow(A->IsRotationNormalized());
    checkSlow(B->IsRotationNormalized());

    //  When Q = quaternion, S = single scalar scale, and T = translation
    //  QST(A) = Q(A), S(A), T(A), and QST(B) = Q(B), S(B), T(B)

    //  QST (AxB) 

    // QST(A) = Q(A)*S(A)*P*-Q(A) + T(A)
    // QST(AxB) = Q(B)*S(B)*QST(A)*-Q(B) + T(B)
    // QST(AxB) = Q(B)*S(B)*[Q(A)*S(A)*P*-Q(A) + T(A)]*-Q(B) + T(B)
    // QST(AxB) = Q(B)*S(B)*Q(A)*S(A)*P*-Q(A)*-Q(B) + Q(B)*S(B)*T(A)*-Q(B) + T(B)
    // QST(AxB) = [Q(B)*Q(A)]*[S(B)*S(A)]*P*-[Q(B)*Q(A)] + Q(B)*S(B)*T(A)*-Q(B) + T(B)

    //  Q(AxB) = Q(B)*Q(A)
    //  S(AxB) = S(A)*S(B)
    //  T(AxB) = Q(B)*S(B)*T(A)*-Q(B) + T(B)
    checkSlow(VectorGetComponent(A->Scale3D, 3) == 0.f);
    checkSlow(VectorGetComponent(B->Scale3D, 3) == 0.f);

    if (Private_AnyHasNegativeScale(A->Scale3D, B->Scale3D))
    {
        // @note, if you have 0 scale with negative, you're going to lose rotation as it can't convert back to quat
        MultiplyUsingMatrixWithScale(OutTransform, A, B);
    }
    else
    {
        const TransformVectorRegister QuatA = A->Rotation;
        const TransformVectorRegister QuatB = B->Rotation;
        const TransformVectorRegister TranslateA = A->Translation;
        const TransformVectorRegister TranslateB = B->Translation;
        const TransformVectorRegister ScaleA = A->Scale3D;
        const TransformVectorRegister ScaleB = B->Scale3D;

        // RotationResult = B.Rotation * A.Rotation
        OutTransform->Rotation = VectorQuaternionMultiply2(QuatB, QuatA);

        // TranslateResult = B.Rotate(B.Scale * A.Translation) + B.Translate
        const TransformVectorRegister ScaledTransA = VectorMultiply(TranslateA, ScaleB);
        const TransformVectorRegister RotatedTranslate = VectorQuaternionRotateVector(QuatB, ScaledTransA);
        OutTransform->Translation = VectorAdd(RotatedTranslate, TranslateB);

        // ScaleResult = Scale.B * Scale.A
        OutTransform->Scale3D = VectorMultiply(ScaleA, ScaleB);
    }
}

父节点全局位置和当前节点在父节点下的局部位置计算当前节点在World Space下的Position代码可写为:

mDerivedPosition = parentOrientation * (DBVector3(parentScale) * mPosition) + parentPosition

当均匀缩放时,mPosition受父节点Scale的影响在每个方向上都相同,所以接下来无论怎么进行旋转变化,X,Y,Z的单位增量都相同。
当非均匀缩放时候,如scale=(2,1,1).mPosition先应用Scale在x轴上的Step变为2,然后应用旋转绕Y轴旋转-90度,此时x轴来到z轴的位置,z轴来到-x轴的位置,所以在全局坐标系下,当前节点的增量为2的坐标轴从x轴变成了z轴。

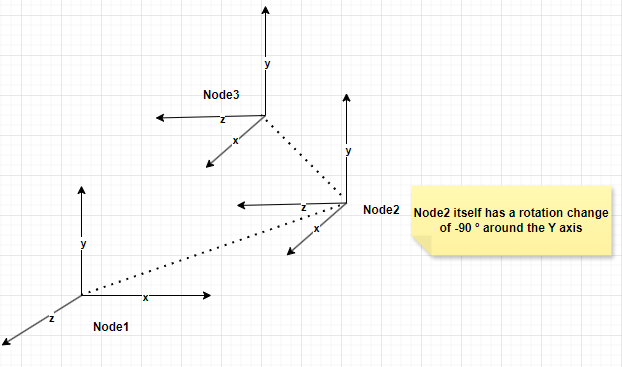
CoordinateTransform

以Node1作为全局坐标系,当scale=(2,1,1)作用于父节点Node1时,x轴的位移被拉长了2倍。

然后Node2进行变化，Node2位置 = Node1位置 + Node1旋转 × (Node1缩放 × Node2局部位置)。

此时Node2在全局坐标系下非均匀缩放变化的依旧是X轴。

接着Node3变化时候,先Scale变化X轴,再旋转X轴来到Z轴的位置上,所以在全局坐标系下,原来X轴的Scale变化变成了Z轴的Scale变化。当scale = (2,1,1)时,由于旋转的影响,此时以Node2节点为分界,Node2之上的节点在全局坐标系下变化的都是X轴,但Node2之下的节点在全局坐标系下变化的实际是Z轴。

(先绕Y轴旋转90度,再沿X轴缩放2倍) 由[1,1,1]变化为[1,1,-2],实际变化的是Z轴值。

\begin{matrix} v \cdot ScaleMatrix \cdot Orientation = [\begin{matrix} 1 & 1 & 1 \end{matrix}] [\begin{matrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} c o s (90) & 0 & s i n (90) \\ 0 & 1 & 0 \\ - s i n (90) & 0 & c o s (90) \end{matrix}] = [\begin{matrix} 1, 1, - 2 \end{matrix}] \end{matrix}

如下图,以向量/四元数组合的方式进行计算。

root节点:其局部坐标系为单位正交坐标系，未施加任何变换。

node1节点:相对于其父节点（即根节点），施加了位移变换 (1, 1, 1) 和旋转变换：绕其局部 Y 轴旋转 90 度。

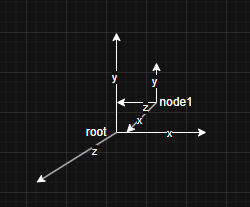
root_node

node1节点中存在一点q,在node1节点下的localPosition为(1,1,1) 在root节点下的DerivedPosition为(2,2,0)。

\begin{matrix} q (derivedPosition) = node 1 (derivedOrientation) \cdot (node 1 (derivedScale) \cdot q (localposition)) + node 1 (derivedPosition) \\ = [\begin{matrix} c o s (90) & 0 & s i n (90) \\ 0 & 1 & 0 \\ - s i n (90) & 0 & c o s (90) \end{matrix}] [\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}] + [\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}] = [\begin{matrix} 2 \\ 2 \\ 0 \end{matrix}] \end{matrix}

若把root挂在了一个scene节点下,且scene存在一个(2,1,1)的缩放。即应用一个scale=(2,1,1)的缩放变化于root坐标系。此时root和node1的变化为:

\begin{matrix} root (derivedScale) = [\begin{matrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] \\ node 1 (derivedPosition) = root (derivedOrientation) \cdot （ root (derivedScale) \cdot node 1 (localPosition) ） + root (derivedPosition) \\ = [\begin{matrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] \cdot [\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}] = [\begin{matrix} 2 \\ 1 \\ 1 \end{matrix}] \\ node 1 (derivedScale) = root (derivedScale) * node 1 (localScale) = [\begin{matrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] \\ node 1 (derivedOrientation) = [\begin{matrix} c o s (90) & 0 & s i n (90) \\ 0 & 1 & 0 \\ - s i n (90) & 0 & c o s (90) \end{matrix}] \end{matrix}

点q的变化此时在scene节点下的DerivedPosition为(3,2,-1)。

\begin{matrix} q (derivedPosition) = node 1 (derivedOrientation) * (node 1 (derivedScale) * q (localPosition)) + node 1 (derivedPosition) \\ = [\begin{matrix} c o s (90) & 0 & s i n (90) \\ 0 & 1 & 0 \\ - s i n (90) & 0 & c o s (90) \end{matrix}] \cdot [\begin{matrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] \cdot [\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}] + [\begin{matrix} 2 \\ 1 \\ 1 \end{matrix}] \\ = [\begin{matrix} 1 \\ 1 \\ - 2 \end{matrix}] + [\begin{matrix} 2 \\ 1 \\ 1 \end{matrix}] = [\begin{matrix} 3 \\ 2 \\ - 1 \end{matrix}] \end{matrix}

再将点q转换到root节点的局部坐标系下坐标为(3/2,2,-1) 与原未进行非均匀缩放变化时,点q在root下的坐标(2,2,0)就不一致了。

\begin{matrix} q (localPosition (root)) = (root (derivedOrientation)^{- 1} * (p (derivedPosition) - root (derivedPosition))) / root (derivedScale) \\ = \frac{[\begin{matrix} 3 \\ 2 \\ - 1 \end{matrix}]}{[\begin{matrix} 2 \\ 1 \\ 1 \end{matrix}]} = [\begin{matrix} 3 / 2 \\ 2 \\ - 1 \end{matrix}]! = [\begin{matrix} 2 \\ 2 \\ 0 \end{matrix}] \end{matrix}

基于父节点坐标系进行的向量/四元数变化组合计算的方式,使得节点的缩放依赖于父节点的旋转方向，导致与期望全局坐标系下进行X轴缩放后的Position不一致。

该例中,期望的是root坐标系下所有的X轴数据发生改变,但当该缩放应用到q时,点q受到父节点node1的旋转影响,在全局坐标系下缩放变化的实际是Z轴坐标,同时X轴数据由于未进行缩放变化,导致在转换到root坐标系下时,依旧要除缩放因子,反而使得x坐标数据变小。

如下视频所示,使用向量四元数组合计算全局坐标系,非均匀缩放原点处的节点,可以第三个节点由于第二个节点的旋转导致在全局坐标系下缩放的变化轴不再是X轴了(白色字体显示的是全局坐标,红线为X轴,蓝线为Z轴,绿线为Y轴)。

解决方案

尝试了3种解决方式:

1.使用矩阵世界变化,然后分解矩阵


xxxxxxxxxx
glm::mat4 Node::getLocalTransform() const 
{
    glm::mat4 translation = glm::translate(glm::mat4(1.0f), mLocalPosition);
    glm::mat4 rotation = glm::toMat4(mLocalOrientation);
    glm::mat4 scale = glm::scale(glm::mat4(1.0f), mLocalScale);

    return translation * rotation * scale;
}

void Node::updateTransforms(const glm::mat4& parentWorldMatrix) 
{
    const glm::mat4 worldTransform = parentWorldMatrix * getLocalTransform();

    mDerivedPosition = glm::vec3(worldTransform[3]);
    mDerivedScale = glm::vec3
    (
        glm::length(glm::vec3(worldTransform[0])),
        glm::length(glm::vec3(worldTransform[1])),
        glm::length(glm::vec3(worldTransform[2]))
    );
    mDerivedOrientation = glm::quat_cast(worldTransform);

    for (auto& child : mChildren) 
    {
        child->updateTransforms(worldTransform);
    }
}

使用该方法非均匀缩放根节点:

但该方法的存在的问题是,由于缩放和旋转矩阵混合计算,导致最后从WorldTransform矩阵提取出来的DerivedScale和DerivedOrientation的值与原先构成该WorldTransform的DerivedScale和DerivedOrientation的值不一致。

2.先旋转再缩放(不太确定可行性)，当应用缩放的节点存在旋转变化时,期望缩放变化轴向也会发生变化,如scale=(2,1,1) 存在一个绕Y轴顺时针旋转九十度的旋转变化,以矩阵乘法 Translate * Rotation * Scale为准,该节点的期望缩放变化轴向是Z轴,但使用该方法始终变化的是X轴。


xxxxxxxxxx
 mDerivedPosition = DBVector3(parentScale) * (parentOrientation * mPosition) + parentPos;

均匀缩放下与原方法效果一致,此时RS的乘法是可交换的。

RS = RsI = sIR = SR

3.把所有节点的Transform转化到实际变化的节点空间下进行计算,类似UE5.4 Dragon IK插件在计算IK时,需要先取角色所有骨骼在模型空间下Transform的方法。


xxxxxxxxxx
glm::vec3 Node::converPositionLocalToWorld(glm::vec3& position)
{
    return mDerivedPosition + (mDerivedOrientation * (mDerivedScale * position));
}

void transformNodeToWorld(std::shared_ptr<Node> node, std::shared_ptr<Node> transform)
{
    if (node == nullptr) { return; }
    glm::vec3 mDerivedPosition = node->getDerivedPosition();
    glm::quat mDerivedOrientation = node->getDerivedOrientation();
    glm::vec3 mDerivedScale = node->getDerivedScale();

    node->setDerivedPosition(transform->converPositionLocalToWorld(mDerivedPosition));
    node->setDerivedOrientation(transform->converOrientationLocalToWorld(mDerivedOrientation));
    node->setDerivedScale(transform->converScaleLocalToWorld(mDerivedScale));

    std::vector<std::shared_ptr<Node>> vec = node->getChildNodes();
    for (const auto& item : vec)
    {
        transformNodeToWorld(item, transform);
    }
}

此时得到的效果与矩阵计算的效果一致,且没有矩阵无法还原缩放和旋转值的问题。

引用

1.Unreal5.4的部分代码

联系方式

电子邮箱:2574308236@qq.com